세포 자동자

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 종류
4. 응용
5. 추가 정보
참조

1. 개요

세포 자동자는 공간을 채운 셀들의 집합으로, 각 셀의 상태가 이웃 셀들의 상태에 따라 결정되는 이산적인 모델이다. 1940년대 존 폰 노이만과 스타니슬라프 울람에 의해 처음 제시되었으며, 자기 복제 시스템 연구와 액체의 움직임 계산을 위한 아이디어에서 시작되었다. 세포 자동자는 초기 연구를 통해 동적 시스템, 기호 역학과의 연결이 이루어졌고, 1970년대 존 호턴 콘웨이의 생명 게임이 등장하며 널리 알려졌다. 스티븐 울프럼은 세포 자동자를 4가지 클래스로 분류하고, 튜링 완전성을 연구했다. 세포 자동자는 생물학, 화학, 물리학, 컴퓨터 과학 등 다양한 분야에서 모델링과 시뮬레이션 도구로 활용되며, 디지털 물리학 분야에서도 우주를 설명하는 가설로 연구되고 있다.

더 읽어볼만한 페이지

세포 자동자 - 라이프 게임
라이프 게임은 존 호턴 콘웨이가 발표한 세포 자동자로, 2차원 격자에서 셀들이 이웃 셀과의 상호작용을 통해 생존, 사멸, 탄생하며 다양한 패턴을 만들고 튜링 완전성을 가진다.
세포 자동자 - 와이어월드
와이어월드는 네 가지 상태를 가진 2차원 세포 자동자이며, 주변 세포의 상태에 따라 변화하는 규칙을 통해 논리 회로, 논리 게이트, 튜링 머신 등을 구현할 수 있다.
체계 이론 - 사이버네틱스
사이버네틱스는 동물과 기계의 제어 및 통신을 연구하는 학문으로, 제어 시스템, 신경과학 등 다양한 분야를 통합하여 발전해왔으며, 피드백, 자기조직화 등의 핵심 개념을 통해 여러 분야에 응용되고 있다.
체계 이론 - 사회 연결망
사회 연결망 분석은 개인이나 집단 간의 관계를 분석하여 사회적 구조와 행동을 이해하는 학제 간 연구 방법론으로, 다양한 이론적 틀을 활용하여 네트워크 내 위치와 정보 접근의 중요성을 분석하며 여러 분야에서 활용된다.

세포 자동자
개요
규칙 184에 따른 셀룰러 오토마타의 진화. 각 행은 시간의 한 단계를 나타낸다.
유형	이산 모델
연구 분야	수학 물리학 복잡계 과학 이론생물학 컴퓨터 과학
발견 시기	1940년대
창시자	스타니스와프 마르친 울람
공동 창시자	존 폰 노이만
상세 정보
정의	셀룰러 오토마타(영어: cellular automaton, 복수형: cellular automata)는 공간과 시간 모두 이산적인 값으로 표현되는 계산 모델이다.
구성 요소	셀(cell): 기본적인 단위 상태(state): 각 셀이 가질 수 있는 값 이웃(neighborhood): 특정 셀에 영향을 주는 주변 셀들의 집합 규칙(rule): 각 셀의 다음 상태를 결정하는 함수
작동 방식	각 셀은 자신의 현재 상태와 이웃 셀들의 상태를 기반으로 규칙에 따라 다음 상태를 결정한다. 이 과정이 모든 셀에 동시에 적용되어 전체 시스템의 상태가 업데이트된다.
특징	병렬 처리: 각 셀은 독립적으로 상태를 업데이트하므로 병렬 처리에 적합하다. 단순한 규칙에서 복잡한 패턴 생성: 간단한 규칙으로도 복잡하고 예측 불가능한 패턴을 생성할 수 있다. 전체론적 행동: 각 셀의 상호작용이 전체 시스템의 행동에 영향을 미친다.
역사
기원	스타니스와프 마르친 울람이 1940년대에 자기 복제 기계에 대한 수학적 모델을 연구하면서 구상되었다.
발전	존 폰 노이만이 울람의 아이디어를 발전시켜 최초의 셀룰러 오토마타 모델을 제시했다. 폰 노이만은 이 모델을 사용하여 자기 복제 기계의 가능성을 탐구했다.
주목할 만한 연구	존 호턴 콘웨이의 라이프 게임은 셀룰러 오토마타의 대중적인 인기를 높이는 데 기여했다. 스티븐 울프럼은 셀룰러 오토마타의 다양한 클래스와 복잡성에 대한 연구를 수행했다.
예시
라이프 게임	간단한 규칙을 가지지만 복잡한 패턴을 생성할 수 있는 대표적인 셀룰러 오토마타이다.
규칙 184	교통 흐름 모델링에 사용되는 셀룰러 오토마타이다.
기본 셀룰러 오토마타	1차원 셀룰러 오토마타로, 각 셀은 두 가지 상태(0 또는 1)를 가질 수 있으며, 자신의 상태와 이웃 셀의 상태에 따라 다음 상태를 결정한다.
기타	다양한 형태의 셀룰러 오토마타가 존재하며, 각기 다른 규칙과 구조를 가진다.
응용 분야
물리학	유체 역학, 결정 성장, 상전이 등 다양한 물리 현상을 모델링하는 데 사용된다.
생물학	세포 성장, 질병 확산, 생태계 모델링 등 생물학적 시스템을 모델링하는 데 사용된다.
컴퓨터 과학	병렬 컴퓨팅, 이미지 처리, 암호학 등 다양한 분야에 응용된다.
기타	사회 과학, 경제학 등 다양한 분야에서 복잡한 시스템을 모델링하고 분석하는 데 사용된다.
참고 문헌
관련 항목
관련 개념	창발성 복잡계 튜링 완전성 자기 복제

2. 역사

세포 자동자의 개념은 1940년대 존 폰 노이만과 스타니스와프 울람에 의해 시작되었다.^[8]^[9]^[85]^[86] 폰 노이만은 자기 복제 기계를 이론적으로 구현하려 했고, 울람은 이를 위한 모델로 이산적인 격자 구조를 제안했다.^[12]^[13]^[89]^[90] 폰 노이만은 이 아이디어를 바탕으로 2차원 격자 공간에서 작동하는 복잡한 세포 자동자 모델을 설계했다.^[15] 비슷한 시기 노버트 위너 등도 관련 연구를 진행했다.^[17]^[94]

1960년대에는 세포 자동자가 동적 시스템 및 기호 역학과 연관되어 수학적으로 연구되기 시작했으며,^[20]^[96] 1969년 콘라트 추제는 우주 전체가 세포 자동자일 수 있다는 디지털 물리학의 아이디어를 제시했다.^[21]^[97] 같은 해 앨비 레이 스미스는 세포 자동자의 계산 능력에 대한 중요한 이론적 기반을 마련했다.^[22]^[23]^[24]

1970년, 존 호턴 콘웨이는 세포 자동자의 가장 유명한 예시인 라이프 게임을 발표하여 큰 반향을 일으켰다.^[157]^[26]^[98] 라이프 게임은 간단한 규칙에도 불구하고 복잡하고 예측 불가능한 패턴을 생성하며, 튜링 완전성을 가진다는 것이 증명되었다.^[27]^[99]

1980년대에는 스티븐 울프럼이 1차원 기본 세포 자동자에 대한 체계적인 연구를 통해 세포 자동자의 행동을 4가지 부류로 분류하고,^[2]^[29] Rule 110과 같은 일부 규칙이 보편적 계산 능력을 가짐을 밝혔다.^[31] 울프럼은 이러한 연구를 바탕으로 세포 자동자가 자연의 복잡성을 이해하는 새로운 도구가 될 수 있다고 주장했다.^[100]

2. 1. 세포 자동자의 탄생과 초기 연구

세포 자동자(Cellular Automata, CA)의 개념은 1940년대 로스앨러모스 국립 연구소에서 활동하던 수학자 스타니스와프 울람과 존 폰 노이만에 의해 처음으로 구체화되었다.^[85]^[86] 당시 울람은 결정의 성장을 연구하기 위해 단순한 격자 네트워크 모델을 사용하고 있었고,^[8]^[85] 폰 노이만은 스스로를 복제하는 기계, 즉 자기 복제 시스템에 대한 이론적 연구를 진행 중이었다.^[9]^[86]

폰 노이만은 1948년 Hixon Symposium에서 발표한 "The general and logical theory of automata^영어"라는 논문^[9] 등을 통해 스스로 복제하는 로봇 모델을 구상했다. 그의 초기 설계는 한 로봇이 다른 로봇을 만드는 방식의 '운동학적 모델'(Kinematic model^영어)이었으나,^[10]^[11]^[87]^[88] 실제 로봇을 만들고 복제에 필요한 부품을 공급하는 과정의 복잡성 때문에 이론적 어려움에 직면했다.^[86] 이때 동료였던 울람은 연속적인 공간 대신, 간단한 유한 오토마타들로 구성된 균일하고 구별된 이산 공간(discrete space)을 사용하여 자기 복제 과정을 추상화된 모델로 연구할 것을 제안했다.^[12]^[13]^[89]^[90] 이 제안이 세포 자동자 개념의 직접적인 출발점이 되었다.

폰 노이만은 울람의 아이디어를 받아들여, 처음에는 3차원 공간을 고려했으나 계산의 편의성을 위해 2차원 격자 공간 모델을 채택했다. 그는 이 2차원 공간의 각 셀(cell)이 29개의 상태를 가질 수 있는 유한 오토마타로 정의하고, 이를 조합하여 '기관'(organ)이라 불리는 다양한 연산 구조를 설계했다.^[15] 그의 궁극적인 목표는 이러한 '기관'들을 이용해 이론적으로 완벽한 자기 복제 오토마타를 구성하는 것이었다. 1950년대에 그는 이 2차원 세포 자동자 내에서 작동하는 폰 노이만 유니버설 생성기를 설계했는데, 이는 약 20만 개의 셀로 구성되어 무한히 자기 복제를 반복할 수 있음을 수학적으로 증명한 것이었다.^[15]^[92] 이 설계는 테셀레이션 모델 또는 폰 노이만 유니버설 생성기라고 불린다.^[16]^[93] 그러나 폰 노이만은 말년에 병을 얻어 이 연구를 완성하지는 못했다. 그럼에도 불구하고 Arthur W. Burks와 같은 후대 연구자들은 폰 노이만의 연구가 실용적인 응용 가능성이 크며, 자기 복제 시스템의 중요한 특징을 보여주는 추상적 모델로서 중요한 의의를 지닌다고 평가했다.^[156]

한편, 폰 노이만과 울람의 연구와 비슷한 시기인 1940년대에 노버트 위너와 아르투로 로젠블루스는 심장 근육에서의 신경 임펄스 전도를 수학적으로 설명하기 위해 모델을 개발했다. 이 모델은 각 지점의 상태가 이웃의 상태에 영향을 받는다는 점에서 세포 자동자와 유사한 특성을 가졌지만,^[17]^[94] 신호가 전파되는 매질을 연속적인 것으로 가정하고 파면(wavefront)이 곡선 형태를 띤다는 점에서 격자 기반의 이산적인 세포 자동자와는 차이가 있었다.^[17]^[18] 진정한 의미의 흥분성 매질에 대한 세포 자동자 모델은 이후 1978년 J. M. 그린버그(Greenberg)와 S. P. 헤이스팅스(Hastings)에 의해 개발되었다.

세포 자동자에 대한 초기 연구는 인공생명 분야의 발전과도 밀접한 관련이 있다. 폰 노이만의 세포 자동자는 최초의 '추상적' 인공 생명 모델 중 하나로 간주되며, 역시 이러한 모델들을 사용하여 초기 인공 생명 현상을 탐구했다.

1960년대에 들어서면서 세포 자동자는 특정 유형의 동적 시스템으로 인식되어 연구되기 시작했으며, 수학의 한 분야인 기호 역학과의 깊은 연관성이 밝혀졌다.^[20] 1969년 구스타프 A. 헤들런드는 이 관점에서 세포 자동자의 수학적 성질들을 체계적으로 정리한 중요한 논문을 발표했다.^[20]^[96] 그의 연구 결과 중 가장 기본적인 것은 Curtis–Hedlund–Lyndon 정리로, 이는 세포 자동자의 전역적인 상태 변화 규칙(global rule)이 위상 공간인 시프트 공간 위에서의 연속 함수 자기사상(endomorphism)과 동일하다는 것을 보여준다.

같은 해인 1969년, 독일의 컴퓨터 선구자 콘라트 추제는 그의 저서 ''계산 공간''(Calculating Space^영어)을 통해 우주의 물리 법칙 자체가 본질적으로 이산적이며, 우주 전체가 하나의 거대한 세포 자동자 위에서 이루어지는 결정론적 계산의 결과일 수 있다는 혁신적인 아이디어를 제시했다. 이는 훗날 디지털 물리학이라는 연구 분야의 중요한 기초가 되었다.^[21]^[97] 또한 컴퓨터 과학자 앨비 레이 스미스는 세포 자동자를 하나의 계산 모델 클래스로서 수학적으로 엄밀하게 다룬 최초의 박사 학위 논문을 완성했다.^[22] 그는 이 연구를 통해 다양한 형태의 이웃(neighborhood) 정의가 본질적으로 동등함을 보였고, 1차원 및 2차원 세포 자동자 모두가 계산적으로 보편적임(computationally universal)을 증명했으며, 폰 노이만의 복잡했던 자기 복제 증명을 1차원 세포 자동자의 계산 보편성 결과를 이용하여 더 간결하게 유도할 수 있음을 보였다.^[22]^[23]^[24]^[25]

2. 2. 라이프 게임의 등장과 대중화

존 폰 노이만으로부터 시작한 셀룰러 오토마타는 이후 다른 과학자들에 의해 활발히 연구되었다. 복잡계나 이론전산학 등에서 종종 연구되며, 인공생명의 맥락에서 생물학에서 연구하기도 한다. 그 중 영국의 수학자 존 콘웨이는 1970년에 셀룰러 오토마타의 가장 훌륭한 예로 평가받는 생명 게임(Game of Life)을 제창하였다.^[157]

'''생명 게임'''은 영국 수학자 존 콘웨이가 만든 게임으로, 플레이어가 없는 zero-player game|제로 플레이어 게임^eng이다. 대신 생명 게임은 초기 상태에서 셀룰러 공간(cellular space)의 어떤 셀(cell)이 '살아있는' 것으로 선택되는가에 따라 그 시스템의 진화 방향이 결정된다. 즉, 초기 상태에 의해서만 결정되는 오토마타이다.

존 콘웨이가 정한 생명 게임의 규칙은 아래와 같은 네 가지뿐이지만, 초기 상태를 어떻게 놓느냐에 따라서 매우 다양하고 "생명 같은"(life-like) 시뮬레이션이 나타난다. (참고로 여기서 '이웃'이란, 2차원 격자 평면에서의 생명 게임의 경우, 한 사각형 셀을 둘러싸고 있는 8개의 셀, 즉 무어 근방을 그 사각형 셀의 '이웃'이라고 정의한다.)

# 현재 살아있는 셀 중 2개 미만의 '이웃'이 살아있는 경우, 과소 상태(under-population)에 의해 그 셀은 다음 상태에 죽는다.

# 현재 살아있는 셀 중 4개 이상의 '이웃'이 살아있는 경우, 과밀 상태(overcrowding)에 의해 그 셀은 다음 상태에 죽는다.

# 현재 살아있는 셀 중 2개 또는 3개의 '이웃'이 살아있는 경우 다음 상태까지 그 셀은 살아남는다.

# 현재 죽은 셀 중 정확히 3개의 '이웃'이 살아있는 경우, 번식(reproduction)에 의해 그 셀은 다음 상태에 살아난다.

이러한 규칙에 따라, 초기 패턴 이후 모든 격자 셀들이 동시에 삶과 죽음이 결정되고, 이러한 모습을 시뮬레이션으로 나타낸 것이 바로 생명 게임이라고 할 수 있다.

비교적 간단한 규칙으로 이루어져 있지만, 생명 게임은 초기 상태에 따라 여러 흥미로운 패턴을 보여준다. 예를 들어 '글라이더(glider)'와 같이 이동하는 패턴이나 '글라이더 건(glider gun)'처럼 글라이더를 계속 생성하는 패턴 등이 발견되었다. "Amazing Game of Life Demo" 영상에서 다양한 패턴 예시를 볼 수 있다.

한편 생명 게임은 규칙의 변형에 따라 단순 격자 형태가 아닌 육각 타일링 구조나 3차원 구조에서도 구현될 수 있다.

이렇게 간단한 규칙들은 아름다운 모양을 만들어 낼 수도 있지만, 자기 복제나 심지어 튜링 완전한 계산까지 할 수 있는 패턴들이 여럿 존재한다. 이는 라이프 게임이 무한한 메모리를 가진 어떤 컴퓨터와도 동등한 계산 능력을 가짐을 의미한다. 또한, '만능 건축사(universal constructor)' 패턴은 튜링 머신과 동등한 컴퓨터를 만들 수 있으며, 이것은 더 복잡한 여러 가지 개체를 만들어내는 데 사용될 수 있다. "LifeWiki"에서 좀 더 자세한 내용을 확인할 수 있다.

2. 3. 스티븐 울프럼의 연구와 분류

1980년대에 스티븐 울프럼(Stephen Wolfram)은 1차원 세포 자동자에 대한 체계적인 연구를 진행했다. 그는 특히 가장 간단한 형태인 초등 셀룰러 오토마타(Elementary Cellular Automata)에 주목했다. 초등 셀룰러 오토마타는 1차원 배열에서 각 셀(cell)이 오직 두 가지 상태(0 또는 1)만을 가지며, 자신의 상태와 바로 양옆 두 이웃 셀의 상태에 따라 다음 세대의 상태가 결정되는 모델이다. 이 규칙은 총 8가지 경우의 수(이전 상태 조합: 111, 110, 101, 100, 011, 010, 001, 000)에 대해 다음 상태(0 또는 1)를 지정하므로, 총 2⁸ = 256개의 가능한 규칙이 존재한다. 울프럼은 이 규칙들을 체계적으로 연구하며 그 행동 양상에 따라 다음과 같은 네 가지 부류(Class)로 분류했다.^[32]^[33]^[34]

클래스 1 (Class 1): 거의 모든 초기 상태에서 빠르게 안정적이고 동일한 상태(모든 셀이 0이거나 모든 셀이 1인 상태)로 수렴한다. 초기 패턴의 무작위성은 사라진다.
클래스 2 (Class 2): 거의 모든 초기 상태에서 안정적인 고정 상태 또는 주기적으로 반복되는 패턴으로 빠르게 수렴한다. 초기 패턴의 일부 정보는 유지될 수 있으며, 국소적인 변화는 주변으로 퍼지지 않고 제한되는 경향이 있다.
클래스 3 (Class 3): 거의 모든 초기 상태에서 혼돈적이고 겉보기에 무작위적인 패턴을 생성한다. 안정적인 구조가 나타나더라도 빠르게 사라지며, 국소적인 변화는 전체 시스템으로 퍼져나가는 경향이 있다.
클래스 4 (Class 4): 거의 모든 초기 상태에서 복잡한 패턴을 생성한다. 국소적인 구조들이 나타나 서로 상호작용하며 오랫동안 지속될 수 있다. 안정적이거나 주기적인 상태로 결국 수렴할 수도 있지만, 그 과정이 매우 길고 예측하기 어렵다. 라이프 게임과 같은 복잡한 행동을 보인다.

울프럼은 특히 클래스 4가 질서와 혼돈의 경계에 있으며, 생명 현상과 같은 복잡계에서 나타나는 복잡한 현상을 설명하는 데 중요하다고 주장했다. 그는 많은 클래스 4 세포 자동자가 보편적 계산(universal computation), 즉 어떤 컴퓨터 프로그램이라도 시뮬레이션할 수 있는 능력을 가질 수 있다고 추측했다.^[33] 이는 이후 Rule 110과 존 콘웨이의 라이프 게임(클래스 4의 대표적인 2차원 예시)에서 실제로 증명되었다.

Rule 110 실행 예시. 복잡한 패턴을 보여주며 튜링 완전함이 증명되었다.

Rule 110은 초등 셀룰러 오토마타의 한 예시로, 다음과 같은 규칙을 따른다. 이 규칙 번호 110은 규칙 표의 '새 상태' 행을 이진수로 읽었을 때(01101110₂) 십진수로 변환한 값이다.

이전 세대 이웃 상태	111	110	101	100	011	010	001	000
다음 세대 셀 상태	0	1	1	0	1	1	1	0

Rule 110 외에도 중요한 초등 셀룰러 오토마타로는 Rule 30이 있는데, 이는 매우 무작위적인 패턴을 생성하여 난수 생성 등에 활용된다.^[158]

울프럼의 분류는 세포 자동자의 행동을 이해하는 중요한 틀을 제공했지만, 이는 본질적으로 정성적인 분류이며 특정 규칙을 어느 클래스로 분류할지에 대한 해석의 여지가 있다.^[34] 그의 분류는 세포 자동자 출력의 압축 길이와 경험적으로 일치하는 경향을 보인다.^[35]

울프럼의 연구 이후, 세포 자동자를 더 형식적이고 엄격하게 분류하려는 시도들이 있었다. 예를 들어, 쿨릭(Kůrka)과 유(Culik)는 세 가지 명확하게 정의된 클래스와 어디에도 속하지 않는 네 번째 클래스를 제안했지만(쿨릭-유 클래스), 특정 규칙이 어떤 클래스에 속하는지를 판정하는 것은 결정 불가능함이 증명되었다.^[36]^[37]^[38]

한편, 울프럼의 4가지 클래스 분류는 노벨상 수상자인 화학자 일리야 프리고진이 제시한 열역학적 시스템의 4가지 분류(평형 상태, 균일 상태, 혼돈 상태, 복잡한 비평형 상태)와 유사성을 보인다.^[40] 울프럼은 이러한 연구 결과를 그의 저서 ''새로운 과학'' (A New Kind of Science) (2002)에서 자세히 설명하며 세포 자동자가 과학의 여러 분야에서 중요한 모델이 될 수 있다고 주장했다.

3. 종류

세포 자동자의 기본 개념은 다양한 방식으로 일반화될 수 있다.

첫째, 셀을 배열하는 격자 구조를 바꿀 수 있다. 일반적인 사각형 격자 대신, 평면을 정육각형으로 타일링하여 육각형 셀을 사용하거나, 펜로즈 타일처럼 불규칙한 격자를 사용할 수도 있다.^[54] 때로는 이러한 비표준 격자 위의 세포 자동자는 특정 이웃 규칙을 가진 사각형 격자 위의 자동자와 동일한 행동을 보이기도 한다.

둘째, 규칙 자체를 변경할 수 있다. 규칙이 결정론적이지 않고 확률적일 수 있는데, 이를 확률적 세포 자동자라고 한다. 확률적 규칙은 특정 패턴에 대해 다음 시간 단계에서 셀이 가질 수 있는 각 상태에 대한 확률을 부여한다. 예를 들어, 생명 게임 규칙을 따르되 매 시간 단계마다 각 셀이 0.001%의 확률로 상태를 바꾸는 식의 규칙도 가능하다. 또한, 규칙이 시간이나 공간에 따라 변할 수도 있다. 예를 들어, 한 세대에서는 수평 이웃 셀의 상태에 따라 다음 상태가 결정되고, 다음 세대에서는 수직 이웃 셀의 상태에 따라 결정되는 방식이다.

셋째, 셀의 상태 업데이트 방식을 변경할 수 있다. 기본적인 세포 자동자에서는 한 셀의 새로운 상태가 다른 셀들의 현재 상태에만 의존하지만, 이를 확장하여 다른 셀들의 새로운 상태에 영향을 받도록 규칙을 만들 수도 있다. 예를 들어, 2x2 셀 블록의 상태가 자신과 주변 셀들에 의해 함께 결정되도록 하는 방식이다.

넷째, 이산적인 상태와 규칙 대신 연속적인 값을 사용할 수 있다. 연속 자동자(Continuous automata^eng)는 상태와 규칙이 연속적인 함수로 정의된다. 셀의 상태는 보통 [0,1 사이의 실수 값을 가지며, 위치 상태는 유한한 개수의 실수로 표현된다. 일부 연속 자동자는 액체 패턴의 확산과 같은 현상을 모델링하는 데 사용될 수 있다. 더 나아가 연속 공간 자동자(Continuous spatial automata^eng)는 셀의 위치 자체도 연속적이다. 시간 역시 연속적이며, 상태는 미분 방정식에 따라 변화한다. 중요한 예로, 앨런 튜링이 얼룩말 줄무늬나 표범 반점 같은 패턴 생성을 설명하기 위해 제안한 반응-확산 시스템이 있다.^[55] 이러한 시스템을 세포 자동자로 근사하면 유사한 패턴이 나타나기도 한다. [http://www.cs.utk.edu/~mclennan/contin-comp.html MacLennan]은 연속 공간 자동자를 계산 모델로 간주한다. 연속 공간 자동자 중에는 생명 게임의 글라이더처럼 전파되는 구조를 보이는 예도 알려져 있다.^[56]

마지막으로, 그래프 재작성 자동자(Graph rewriting automata^eng)는 그래프 재작성 시스템을 기반으로 세포 자동자를 확장한 형태이다.^[57]

3. 1. 기본 세포 자동자 (Elementary Cellular Automata)

기본(또는 초등) 세포 자동자(Elementary Cellular Automata)는 가장 단순한 형태의 세포 자동자로, 1차원 배열의 셀(cell)들로 구성된다. 각 셀은 오직 두 가지 상태(보통 0과 1로 표현)만 가질 수 있으며, 셀의 다음 상태는 현재 자신의 상태와 바로 양옆에 위치한 이웃 셀들의 상태에 따라 결정된다.^[6] 즉, 어떤 셀의 다음 상태를 결정하기 위해 고려하는 이웃은 해당 셀 자신과 왼쪽 셀, 오른쪽 셀의 세 개 셀이다.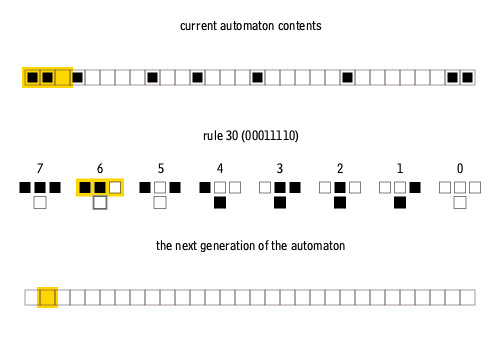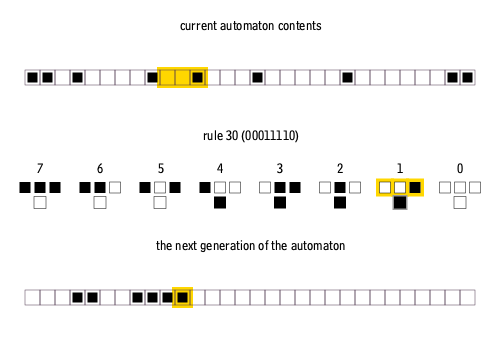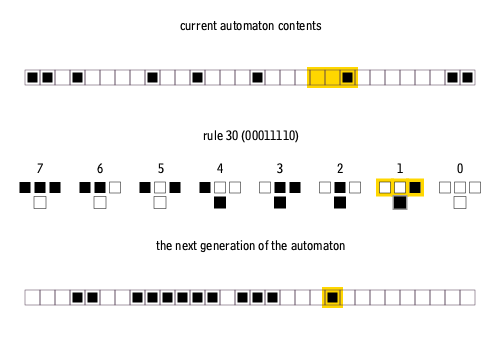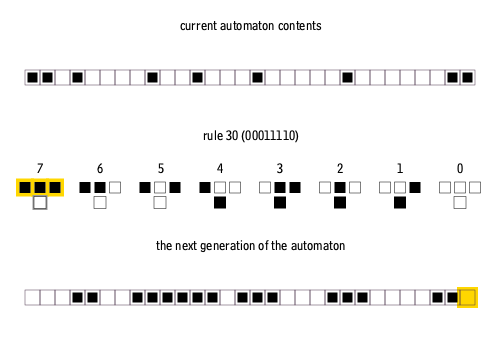

1차원 세포 자동자의 규칙이 다음 세대를 결정하는 방식을 보여주는 애니메이션

세 개의 셀(자신과 양옆 이웃)이 각각 두 가지 상태(0 또는 1)를 가질 수 있으므로, 가능한 이웃 상태 패턴은 2³ = 8가지이다 (예: 111, 110, 101, 100, 011, 010, 001, 000). 각 8가지 패턴에 대해 중앙 셀의 다음 상태가 0 또는 1이 될지를 결정하는 규칙을 정해야 한다. 따라서 가능한 규칙의 총 가짓수는 2⁸ = 256가지이다.^[6]^[83]

이 256개의 규칙들은 스티븐 울프럼이 제안한 울프람 코드(Wolfram code)라는 표준 명명 규칙에 따라 0부터 255까지의 숫자로 구별된다. 이 숫자는 8가지 이웃 패턴(보통 111부터 000 순서)에 대한 다음 상태 값(0 또는 1)을 순서대로 나열하여 얻은 8비트 이진수를 십진수로 변환한 값이다. 예를 들어, Rule 110은 다음과 같은 규칙을 가진다.^[158]

Rule 110 세포 자동자 규칙 (이진수 01101110 = 십진수 110)
현재 패턴 (이웃 상태)	111	110	101	100	011	010	001	000
중앙 셀의 다음 상태	0	1	1	0	1	1	1	0

256개의 규칙 중에는 상태 0과 1을 서로 바꾸거나(complementary rule), 규칙의 좌우를 뒤집었을 때(reflection rule) 동일한 행동을 보이는 경우가 있다. 이러한 대칭성을 고려하면 실질적으로 서로 다른 행동을 보이는 기본 세포 자동자 규칙은 88가지이다.^[158]

기본 세포 자동자는 매우 단순한 모델임에도 불구하고 복잡한 행동을 보일 수 있다. 특히 일부 규칙은 튜링 완전(Turing complete)하다는 것이 증명되었는데, 이는 적절한 초기 상태만 주어진다면 이론적으로 어떤 계산이든 수행할 수 있음을 의미한다. 이런 특성을 가진 규칙을 "범용적"(universal)이라고 부르기도 한다.^[158]

주요 기본 세포 자동자 규칙의 예는 다음과 같다.

Rule 30: 매우 무작위적으로 보이는 패턴을 생성하여 난수 생성 등에 활용된다.^[158] 스티븐 울프럼의 분류에 따르면 '클래스 3' 행동(혼돈적인 패턴)을 보인다. 단순한 초기 상태(예: 중앙에 하나의 1만 있는 상태)에서도 복잡하고 예측하기 어려운 패턴이 나타난다.

Rule 30 세포 자동자 규칙 (이진수 00011110 = 십진수 30)
현재 패턴	111	110	101	100	011	010	001	000
중앙 셀의 다음 상태	0	0	0	1	1	1	1	0

Rule 110: 생명 게임과 유사하게 국소적인 구조들이 나타나 서로 복잡하게 상호작용하는 '클래스 4' 행동을 보인다.^[158] 1994년, 당시 울프럼의 연구 조교였던 매튜 쿡(Matthew Cook)은 Rule 110이 튜링 완전하다는 것을 증명했다. 이는 매우 단순한 1차원 시스템임에도 불구하고 보편적인 계산 능력을 가지고 있음을 보여주는 중요한 결과이다.^[58]^[125] 쿡은 1998년 산타페 연구소(Santa Fe Institute) 학회에서 이 증명을 발표했지만, 울프럼이 그의 저서 ''새로운 종류의 과학(A New Kind of Science)'' 출판 전에 세부 내용이 공개되는 것을 원치 않아 발표가 지연되었고, 2004년에야 울프럼의 저널 ''복잡계(Complex Systems)''에 정식으로 게재되었다.^[58]^[125] Rule 110은 알려진 가장 작은 범용 튜링 기계 중 하나의 기반이 되었다.^[59]^[126]

Rule 110 세포 자동자 규칙 (이진수 01101110 = 십진수 110)
현재 패턴	111	110	101	100	011	010	001	000
중앙 셀의 다음 상태	0	1	1	0	1	1	1	0

3. 2. 총체적 세포 자동자 (Totalistic Cellular Automata)

세포 자동자 중 특별한 종류로 총체적 세포 자동자(Totalistic Cellular Automata^eng)가 있다. 총체적 세포 자동자에서는 각 셀의 상태가 숫자로 표현되며(보통 유한 집합의 정수 값), 시간 ''t''에서의 셀 값은 이전 시간 ''t''-1에서의 주변 셀 값들의 합에 의해서만 결정된다.^[50]^[51]^[118]

만약 시간 ''t''에서의 셀 상태가 이전 시간 ''t''-1에서의 자신의 상태와 주변 이웃 셀 값들의 합 모두에 의존한다면, 이를 외부 총체적 세포 자동자(Outer Totalistic Cellular Automata^eng)라고 부른다.^[51]^[119] 콘웨이의 생명 게임은 셀 값이 0과 1인 외부 총체적 세포 자동자의 한 예시이다.^[51]^[119] 콘웨이의 생명 게임과 동일한 무어 이웃 구조를 가지면서 외부 총체적 규칙을 따르는 다른 세포 자동자들을 생명체와 유사한 세포 자동자(life-like cellular automata)라고 부르기도 한다.^[52]^[53]^[120]^[121]

3. 3. 가역적 세포 자동자 (Reversible Cellular Automata)

세포 자동자는 모든 현재 세포 자동자 구성에 대해 정확히 하나의 과거 구성(전사상)이 있다면 가역적(reversible^eng)이라고 한다.^[41]^[109] 세포 자동자를 구성을 구성으로 매핑하는 함수로 생각한다면, 가역성은 이 함수가 전단사 함수임을 의미한다.^[41]^[109] 세포 자동자가 가역적이라면 시간 반전된 동작도 세포 자동자로 설명할 수 있다. 이 사실은 세포 자동자의 위상학적 특성인 커티스-헤들런드-린든 정리의 결과이다.^[42]^[43]^[110]^[111] 모든 구성이 전사상을 갖지 않는 세포 자동자의 경우, 전사상이 없는 구성을 ''에덴 동산 패턴''이라고 한다.^[44]^[112]

1차원 세포 자동자의 경우 규칙이 가역적인지 비가역적인지를 결정하는 알려진 알고리즘이 있다.^[45]^[46]^[113]^[114] 그러나 2차원 이상의 세포 자동자의 경우 가역성은 결정 불가능 문제이다. 즉, 자동자 규칙을 입력으로 받아 자동자가 가역적인지 여부를 올바르게 결정하도록 보장하는 알고리즘은 없다. 야르코 카리의 증명은 왕 타일에 의한 타일링 문제와 관련이 있다.^[47]^[115]

가역적 세포 자동자는 열역학 법칙을 따르기 때문에 가스 및 유체 역학과 같은 물리적 현상을 시뮬레이션하는 데 자주 사용된다. 이러한 세포 자동자는 가역적으로 특별히 구성된 규칙을 가지고 있다. 이러한 시스템은 토마소 토폴리, 노먼 마골러스 등에 의해 연구되었다. 알려진 역함수를 가진 가역적 세포 자동자를 명시적으로 구성하는 데 사용할 수 있는 몇 가지 기술이 있다. 두 가지 일반적인 기술은 second order cellular automaton|2차 세포 자동자^eng와 block cellular automaton|블록 세포 자동자^eng인데, 이 두 가지 모두 세포 자동자의 정의를 어떤 방식으로 수정하는 것을 포함한다. 이러한 자동자는 위에서 주어진 정의를 엄격하게 만족하지 않지만, 충분히 큰 이웃과 상태 수를 가진 기존 세포 자동자로 에뮬레이션될 수 있으며 따라서 기존 세포 자동자의 하위 집합으로 간주될 수 있다는 것을 보여줄 수 있다. 반대로, 모든 가역적 세포 자동자는 블록 세포 자동자로 에뮬레이션될 수 있다는 것이 밝혀졌다.^[48]^[49]^[116]^[117]

4. 응용

세포 자동자는 다양한 과학 및 공학 분야에서 현상을 모델링하고 시뮬레이션하는 도구로 활용된다.

'''생물학'''

여러 생물학적 과정이 세포 자동자를 통해 설명되거나 시뮬레이션될 수 있다.

조개 껍데기 패턴: ''고둥''속과 ''Cymbiola''속 같은 일부 조개의 껍데기 무늬는 자연적인 세포 자동자 활동의 결과로 여겨진다. 껍데기 가장자리의 색소 세포들이 주변 세포와의 상호작용(활성화 및 억제) 규칙에 따라 색소를 분비하며, 껍데기가 성장함에 따라 패턴이 형성된다.^[61]^[127] 특히 ''Conus textile''(거문고고둥)의 무늬는 스티븐 울프럼이 연구한 규칙 30 세포 자동자와 유사성이 관찰된다.^[61]^[127]
식물 기체 교환: 식물 잎의 각 기공은 주변 기공의 상태에 영향을 받아 열리고 닫히며 가스 교환을 조절하는데, 이는 세포 자동자 메커니즘으로 모델링될 수 있다.^[62]^[128]
두족류 피부 패턴: 오징어나 문어와 같은 두족류는 피부의 색소포를 확장하거나 수축시켜 몸 색깔과 패턴을 빠르게 바꾸는데, 이 움직이는 패턴 변화는 각 색소포를 셀로 하는 2차원 세포 자동자로 시뮬레이션할 수 있다.^[63]^[129]
신경 활동: 뉴런의 활동 전위 발생과 전파 과정을 모델링하기 위해 임계값 자동자가 사용되었으며, 이를 통해 인식이나 학습과 같은 복잡한 뇌 활동을 시뮬레이션하려는 연구가 진행되었다.^[64]
세포 거동: 섬유아세포와 같이 주변 세포와 국소적인 상호작용을 통해 집단적 행동을 보이는 세포들의 움직임은 세포 자동자와 유사한 측면이 있다.^[65]^[130]
종양 모델링: 세포의 증식, 이동, 상호작용을 모델링하는 생물학적 격자 기체 세포 자동자(BIO-LGCA)와 같은 확장된 모델을 사용하여, 암세포의 전이 과정^[66], 종양 이질성의 역할^[67], 표현형 전환^[68] 등 복잡한 생물학적 및 의학적 현상을 연구한다.

'''화학'''

벨로우소프-자보틴스키 반응은 세포 자동자로 시뮬레이션할 수 있는 대표적인 시공간적 화학 진동자 현상이다. 특정 화학 물질들을 혼합하면 반응 용액 내에서 동심원이나 나선형의 패턴이 자발적으로 생성되어 퍼져나가는데, 이는 각 지점의 화학적 상태가 주변 지점의 상태에 따라 변화하는 과정으로 이해될 수 있다. 그린버그-헤이스팅스 모델이나 마틴 게르하르트와 하이케 슈스터가 개발한 세포 자동자 모델^[70]^[132] 등은 이러한 화학 반응의 패턴 형성을 성공적으로 재현했다.^[69]^[131]

'''물리학'''

격자 기체 오토마타의 시각화. 각 픽셀의 색상은 해당 위치의 기체 입자 밀도를 나타낸다. 노란색 셀은 경계를 형성한다.

세포 자동자는 물리학의 여러 현상을 모델링하는 데 사용된다. 초기 연구에서는 비선형 화학 반응, 나선 은하의 진화, 수지상 결정의 성장 모델 등에 적용되었다.

통계 물리학 및 응집 물질 물리학: 확률적 세포 자동자는 유체 역학이나 상전이와 같은 현상을 연구하는 데 유용하다.^[71]^[72] 예를 들어, 이징 모형은 각 셀이 '위' 또는 '아래'의 스핀 상태를 가지는 간단한 모델로, 자석의 자화 및 온도 변화에 따른 상전이 현상을 설명하는 데 사용된다. 이러한 모델에서 나타나는 보편성은 서로 다른 물리계(예: 자성체의 상전이와 액체-기체 상전이) 간의 유사성을 이해하는 데 도움을 준다.^[71]^[72] 특히 2차원 임계 이징 모형과 관련된 상전이는 등각장론을 통해 깊이 연구되었다.^[73]
유체 시뮬레이션: 격자 기체 오토마타는 유체 입자의 이산적인 움직임과 충돌 규칙을 기반으로 유체 흐름을 시뮬레이션하는 데 사용되는 세포 자동자의 한 종류이다.

'''컴퓨터 과학'''

세포 자동자는 컴퓨터 과학의 이론 및 응용 연구에 다양하게 활용된다. 컴퓨터 공학에서는 병렬 컴퓨터의 모델로 생각하고 패턴 인식과 이미지 처리기로서 응용하려는 시도도 있다.

병렬 컴퓨팅 모델: 각 셀이 동시에 독립적으로 계산을 수행하는 세포 자동자의 특성은 병렬 컴퓨팅의 자연스러운 모델을 제공한다. 이를 물리적으로 구현하려는 시도로 수축 배열과 같은 세포 자동자 프로세서 구조가 제안되었다.^[74]
패턴 인식 및 이미지 처리: 세포 자동자의 국소적 규칙 기반 상태 변화는 패턴 인식이나 이미지 처리 알고리즘 개발에 영감을 주었다.
의사 난수 생성: Rule 30과 같은 특정 규칙의 세포 자동자는 복잡하고 예측하기 어려운 패턴을 생성하여 의사 난수 생성기로 사용될 수 있다.^[75]^[137] 2차원 세포 자동자 또한 난수 생성에 활용된다.^[75]
암호학: Rule 30은 초기 상태로부터의 변화는 예측 가능하지만 역추적이 어려운 특성 때문에 블록 암호에 응용될 가능성이 제기되었다.^[138] 또한, 특정 유한 세포 자동자의 진화 과정이 일방향 함수처럼 작동할 수 있다는 점에 착안하여 공개 키 암호화에 활용하려는 제안도 있었다.^[139]
오류 정정 부호: 세포 자동자를 이용하여 오류 정정 부호(CAECC)를 설계하고 고속 하드웨어 디코더를 구현하는 연구가 수행되었다.^[76]
이론적 문제 해결: 사격 분대 동기화 문제나 다수결 문제와 같은 분산 컴퓨팅 환경의 고전적인 문제들을 세포 자동자 모델로 해결하려는 연구가 있다.
창발 계산: 멜라니 미첼 등은 유전자 알고리즘과 같은 진화 연산 기법을 사용하여 특정 작업을 수행하도록 세포 자동자의 규칙을 진화시키는 연구를 수행했다. 이는 분산 시스템에서 복잡한 문제 해결 능력이 어떻게 창발하는지를 탐구하는 창발 계산 분야와 관련된다.^[133]^[134]^[135]^[136]

'''생성 예술 및 음악'''

세포 자동자의 규칙 기반 패턴 생성 능력은 예술 및 엔터테인먼트 분야에서도 활용된다.

음악: 생성 음악^[77]이나 진화 음악 작곡 시스템에서 세포 자동자를 사용하여 예측 불가능하면서도 구조적인 음악 패턴을 만드는 데 사용된다.^[78]
시각 예술 및 게임: 비디오 게임에서 절차적 지형이나 텍스처를 생성하거나^[79], 생성 예술 작품의 패턴 생성 엔진으로 활용된다.

'''기타'''

세포 자동자의 원리는 미로 생성 알고리즘과 같이 특정 조건을 만족하는 구조를 생성하는 문제 해결에도 응용될 수 있다.

5. 추가 정보

세포 자동자의 개념은 다양한 방식으로 확장될 수 있다.

첫째, 격자의 형태를 바꿀 수 있다. 일반적인 사각형(또는 3차원의 입방체) 격자 대신 다른 도형을 사용할 수 있다. 예를 들어 평면을 정육각형으로 타일링하여 각 육각형을 셀로 사용할 수 있다. 많은 경우, 이렇게 만들어진 세포 자동자는 적절히 주변 환경과 규칙을 조정한 사각형 격자 세포 자동자와 동일하게 작동한다. 또한, 펜로즈 타일처럼 격자 자체를 불규칙하게 만들 수도 있다.^[54]^[122]

둘째, 규칙을 결정론적이 아닌 확률적으로 만들 수 있다. 이러한 세포 자동자를 확률적 세포 자동자라고 부른다. 확률적 규칙은 시간 ''t''의 특정 패턴에 대해, 다음 시간 ''t'' + 1에서 중심 셀이 가질 수 있는 각 상태로 변할 확률을 지정한다. 때로는 "기본 규칙은 생명 게임과 같지만, 각 시간 단계마다 0.001%의 확률로 셀의 상태(색상)가 반전된다"와 같이 더 간단한 확률 규칙을 사용하기도 한다.

셋째, 주변 환경의 정의나 규칙이 시간이나 공간에 따라 변하도록 할 수 있다. 예를 들어, 첫 번째 세대에서는 수평 방향의 이웃 셀에 따라 상태가 결정되지만, 다음 세대에서는 수직 방향의 이웃 셀에 따라 결정되도록 규칙을 바꿀 수 있다.

넷째, 업데이트 방식을 변경할 수 있다. 일반적인 세포 자동자에서는 한 셀의 새로운 상태가 다른 셀들의 '현재' 상태에만 의존하며, 다른 셀들의 '새로운' 상태에는 영향을 받지 않는다. 이 원칙을 변경하여, 예를 들어 2x2 크기의 셀 블록 전체의 다음 상태가 그 블록 자체와 주변 셀들의 현재 상태에 의해 함께 결정되도록 할 수도 있다.

다섯째, 상태 값을 이산적인 것 대신 연속적인 값으로 확장한 '연속값 세포 자동자'도 있다. 이는 전체론적 세포 자동자와 유사하지만, 규칙과 상태가 {0, 1, 2}와 같은 이산적인 값이 아니라 연속 함수를 사용하며, 상태 값도 연속적이다(보통 단위 구간 [0, 1] 사이의 값을 가짐). 즉, 각 셀의 상태는 유한한 개수의 실수로 표현된다. 특정 세포 자동자는 이러한 방식으로 액체의 확산과 같은 패턴을 모델링하는 데 사용될 수 있다.

여섯째, 위치 자체를 연속적으로 다루는 '연속 공간 자동자'도 있다. 위치와 시간이 모두 연속적이며, 상태는 미분 방정식에 따라 변화한다. 중요한 예시 중 하나는 반응-확산 시스템으로, 앨런 튜링은 얼룩말의 줄무늬나 표범의 반점 같은 생물학적 패턴이 형성되는 화학 반응을 설명하기 위해 관련 미분 방정식을 제안했다.^[55]^[123] 세포 자동자를 이용해 이러한 패턴을 근사적으로 생성할 수도 있다. 연속 공간 자동자 중에는 생명 게임의 글라이더처럼 특정 패턴이 전파되는 현상을 보이는 예도 알려져 있다.^[56]^[124]

일곱째, 그래프 재작성 시스템을 기반으로 하는 '그래프 재작성 자동자'와 같은 확장도 존재한다.^[57]

=== 디지털 물리학 ===

콘라트 추제(Konrad Zuse)는 1969년 그의 저서 ''Calculating Space''에서 우주 전체가 거대한 세포 자동자의 결정론적 결과일 수 있다는 아이디어를 제시했다. 이 책은 오늘날 디지털 물리학 분야의 시초로 평가받는다.

앤드루 일라친스키(Andrew Ilachinski)는 그의 저서 ''세포 자동자(Cellular Automata)''에서 많은 학자들이 우주 자체가 세포 자동자일 수 있다는 가능성에 대해 의문을 제기해왔다고 지적했다.^[140] 그는 이 문제의 중요성을 이해하기 위해, 예를 들어 규칙 110과 같은 단순한 1차원 세포 자동자가 시간이 지남에 따라 만들어내는 복잡한 패턴을 어떻게 설명할 수 있을지 생각해보는 것이 도움이 된다고 주장했다.^[141] 만약 그 패턴이 어떻게 생성되었는지 모른다면, 마치 어떤 입자 같은 객체들이 상호작용하며 움직이는 궤적처럼 보일 수 있다는 것이다. 실제로 물리학자 제임스 크러치필드(James Crutchfield)는 이러한 관찰을 바탕으로 엄밀한 수학적 이론을 구축하기도 했다.^[142] 이러한 생각을 더 발전시키면, 소립자 물리학에서 다루는 우리 우주의 근본적인 작동 방식 역시 세포 자동자로 이해할 수 있지 않을까 하는 가설에 도달하게 된다.

이러한 아이디어에 기반한 이론은 아직 발전 중이지만, 많은 학자들이 이 가설에 흥미를 느끼고 세계를 이산적인 틀로 이해하려는 시도를 통해 흥미로운 추측과 유용한 직관을 제시하고 있다. 인공지능(AI) 연구의 선구자인 마빈 민스키(Marvin Minsky)는 4차원 세포 자동자 격자 위에서 소립자들의 상호작용을 이해하는 방법을 연구했다.^[143] 컴퓨터의 선구자 콘라트 추제는 소립자가 정보를 어떻게 보유하는지에 대한 문제를 해결하기 위해 불규칙한 격자 구조를 고안하기도 했다.^[144] 에드워드 프레드킨(Edward Fredkin)은 "유한 본성 가설(finite nature hypothesis)"을 제창하며, "궁극적으로 시간과 공간을 포함한 모든 물리량은 이산적이고 유한하다는 것이 밝혀질 것"이라고 주장했다.^[145] 프레드킨과 스티븐 울프럼은 디지털 물리학의 주요 지지자들이다.

21세기에 들어서도 이러한 아이디어는 계속 탐구되고 있다. 울프럼은 그의 저서 ''새로운 종류의 과학''에서 세포 자동자가 물리학을 포함한 다양한 분야를 이해하는 핵심 열쇠라고 주장했다. 또한, 프란체스코 베르토(Francesco Berto) 등이 발전시킨 iLabs^[146]는 2010년 ''Mathematics Of the Models of Reference''라는 저작에서 "마름모십이면체" 격자와 독특한 규칙을 기반으로 2차원 및 3차원 우주를 설명하는 모델을 제안했다. 이 모델은 튜링 머신과 동등한 계산 능력을 가지며, 완전한 가역성(정보 손실 없이 과거 상태 복원 가능)을 지니고, 우주의 발전에 대한 정성적인 설명을 계산할 수 있는 논리 체계를 갖추고 있다고 알려져 있다.^[147]

참조

_[1] 서적 Darwin's Dangerous Idea Penguin Books
_[2] 학술지 Statistical Mechanics of Cellular Automata http://www.stephenwo[...] 2011-02-28
_[3] 서적 Cellular Automata Machines: A New Environment for Modeling https://books.google[...] MIT Press
_[4] 서적 Cellular Automata: A Discrete View of the World https://books.google[...] Wiley & Sons, Inc
_[5] 간행물
_[6] 간행물
_[7] 간행물
_[8] 서적 The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics https://archive.org/[...] Sterling Publishing Company, Inc
_[9] 간행물
_[10] 문서 "The general and logical theory of automata," in [[Lloyd A. Jeffress|L.A. Jeffress]], ed., Cerebral Mechanisms in Behavior – The Hixon Symposium John Wiley & Sons
_[11] 학술지 Man viewed as a machine
_[12] 간행물
_[13] 간행물
_[14] 간행물
_[15] 간행물
_[16] 간행물
_[17] 학술지 The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle
_[18] 학술지 N. Wiener's theory of the activity of excitable media
_[19] 학술지 Stationary and drifting spiral waves of excitation in isolated cardiac muscle
_[20] 학술지 Endomorphisms and automorphisms of the shift dynamical system
_[21] 간행물
_[22] 웹사이트 Cellular Automata Complexity Trade-Offs http://alvyray.com/P[...]
_[23] 웹사이트 Simple Computation-Universal Cellular Spaces http://alvyray.com/P[...]
_[24] 웹사이트 Simple Nontrivial Self-Reproducing Machines http://alvyray.com/P[...]
_[25] 웹사이트 Introduction to and Survey of Cellular Automata or Polyautomata Theory http://alvyray.com/P[...]
_[26] 학술지 Mathematical Games: The fantastic combinations of John Conway's new solitaire game "life" http://www.ibiblio.o[...]
_[27] 웹사이트 Life universal computer http://www.igblan.fr[...] 2009-09-06
_[28] 간행물
_[29] 간행물
_[30] 간행물
_[31] 학술지 Is the Universe a Universal Computer? 2002-10-04
_[32] 간행물
_[33] 간행물
_[34] 간행물
_[35] 학술지 Compression-based investigation of the dynamical properties of cellular automata and other systems http://www.complex-s[...]
_[36] 서적 Cellular automata: a parallel model Springer
_[37] 서적 Computational analysis of one-dimensional cellular automata https://books.google[...] World Scientific
_[38] 서적 Models of massive parallelism: analysis of cellular automata and neural networks https://archive.org/[...] Springer
_[39] 간행물 The structure of the elementary cellular automata rule space http://www.complex-s[...] 2013-01-25
_[40] 간행물 Dissipative Structures, Catastrophes, and Pattern Formation: A Bifurcation Analysis http://www.complex-s[...] 2017-03-25
_[41] 간행물
_[42] 간행물 Tessellations with local transformations
_[43] 서적 Cellular Automata in Hyperbolic Spaces – Tome I, Volume 1 https://books.google[...] Archives contemporaines
_[44] 간행물
_[45] 간행물 Decision Procedures for Surjectivity and Injectivity of Parallel Maps for Tessellation Structures
_[46] 간행물 De Bruijn Graphs and Linear Cellular Automata http://www.complex-s[...]
_[47] 간행물 Reversibility of 2D cellular automata is undecidable
_[48] 간행물 On the circuit depth of structurally reversible cellular automata
_[49] 간행물 Representing reversible cellular automata with reversible block cellular automata http://www.dmtcs.org[...]
_[50] 간행물
_[51] 서적 Cellular automata: a discrete universe https://books.google[...] World Scientific
_[52] 간행물
_[53] 간행물
_[54] 웹사이트 First gliders navigate ever-changing Penrose universe https://www.newscien[...]
_[55] 서적 Mathematical biology Springer 2003
_[56] 문서 RealLife: The continuum limit of Larger than Life cellular automata 2007-03
_[57] 서적 Adaptive Networks
_[58] 간행물 What Kind of Science is This?
_[59] 간행물 Is the Universe a Computer? http://www.nybooks.c[...] 2012-10-12
_[60] 간행물 Transition phenomena in cellular automata rule space
_[61] 문서 The Geometry and Pigmentation of Seashells http://www.maths.not[...] 2012-09-02
_[62] 간행물 Evidence for complex, collective dynamics and emergent, distributed computation in plants
_[63] 웹사이트 Archived copy http://gilly.stanfor[...] 2008-09-14
_[64] 간행물
_[65] 서적 Disordered Systems and Biological Organization
_[66] 간행물 Cell–cell adhesion and 3D matrix confinement determine jamming transitions in breast cancer invasion 2020-09
_[67] 간행물 Cell adhesion heterogeneity reinforces tumour cell dissemination: novel insights from a mathematical model 2017-08-11
_[68] 간행물 'Go or Grow': the key to the emergence of invasion in tumour progression? https://academic.oup[...] 2012-03-01
_[69] 문서 The hodgepodge machine makes waves 1988-08
_[70] 간행물 A cellular automaton describing the formation of spatially ordered structures in chemical systems
_[71] 서적 Statistical Mechanics: Entropy, Order Parameters, and Complexity http://pages.physics[...] Oxford University Press
_[72] 서적 Statistical Physics of Fields Cambridge University Press
_[73] 간행물 A-D-E Classification of Conformal Field Theories
_[74] 서적 Cellular Automaton Processor Based Systems for Genetic Sequence Comparison/Database Searching Cornell University 1996-08
_[75] 간행물 On the generation of high-quality random numbers by two-dimensional cellular automata
_[76] 간행물 Design of CAECC - cellular automata based error correcting code 1994-06
_[77] 문서 Cellular automata in generative electronic music and sonic art: a historical and technical review https://web2.qatar.c[...] Digital Creativity
_[78] 문서 Evolving cellular automata music: From sound synthesis to composition https://sites.google[...] Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications
_[79] 서적 Proceedings of 6th International Conference in Software Engineering for Defence Applications
_[80] 서적 Darwin's Dangerous Idea Penguin Books, London
_[81] 간행물 Statistical Mechanics of Cellular Automata http://www.stephenwo[...]
_[82] Harvn
_[83] Harvn
_[84] Harvn
_[85] 서적 The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics Sterling Publishing Company, Inc
_[86] Harvn
_[87] 문서 The general and logical theory of automata John Wiley & Sons, New York
_[88] 문서 Man viewed as a machine
_[89] Harvn
_[90] Harvn
_[91] Harvn
_[92] Harvn
_[93] 서적 Theory of Self-Reproducing Automata University of Illinois Press
_[94] 간행물 The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle
_[95] 간행물 Stationary and drifting spiral waves of excitation in isolated cardiac muscle
_[96] 간행물 Endomorphisms and automorphisms of the shift dynamical system http://www.springerl[...]
_[97] Harvn
_[98] 간행물 Mathematical Games: The fantastic combinations of John Conway's new solitaire game "life" http://www.ibiblio.o[...]
_[99] 웹사이트 Life universal computer http://www.igblan.fr[...] 2002-11
_[100] Harvn
_[101] Harvn
_[102] Harvn
_[103] Harvn
_[104] Harvn
_[105] 간행물 Compression-based investigation of the dynamical properties of cellular automata and other systems http://www.complex-s[...]
_[106] 서적 Cellular automata: a parallel model https://books.google[...] Springer
_[107] 서적 Computational analysis of one-dimensional cellular automata https://books.google[...] World Scientific
_[108] 서적 Models of massive parallelism: analysis of cellular automata and neural networks Springer
_[109] 간행물
_[110] 학술지 Tessellations with local transformations
_[111] 서적 Cellular Automata in Hyperbolic Spaces - Tome I, Volume 1 https://books.google[...] Archives contemporaines
_[112] 간행물
_[113] 문서 Decision Procedures for Surjectivity and Injectivity of Parallel Maps for Tessellation Structures
_[114] 학술지 De Bruijn Graphs and Linear Cellular Automata http://www.complex-s[...]
_[115] 학술지 Reversibility of 2D cellular automata is undecidable
_[116] 학술지 On the circuit depth of structurally reversible cellular automata
_[117] 학술지 Representing reversible cellular automata with reversible block cellular automata
_[118] 간행물
_[119] 서적 Cellular automata: a discrete universe https://books.google[...] World Scientific
_[120] 간행물
_[121] 서적 Game of Life Cellular Automata Springer
_[122] 웹사이트 http://www.newscient[...]
_[123] 학술지 Mathematical Biology II 슈プリンガー・サイエンス・アンド・ビジネス・メディア
_[124] 학술지 RealLife: The continuum limit of Larger than Life cellular automata 2007-03
_[125] 학술지 What Kind of Science is This?
_[126] 웹사이트 Is the Universe a Computer? http://www.nybooks.c[...] Rea S. Hederman 2002-10-24
_[127] 웹사이트 The Geometry and Pigmentation of Seashells http://www.maths.not[...] 2009-02-15
_[128] 학술지 Evidence for complex, collective dynamics and emergent, distributed computation in plants http://www.pnas.org/[...]
_[129] 웹사이트 http://gilly.stanfor[...]
_[130] 서적 Disordered Systems and Biological Organization
_[131] 뉴스 The hodgepodge machine makes waves Scientific American 1988-08
_[132] 뉴스 A cellular automaton describing the formation of spatially ordered structures in chemical systems
_[133] 문서 The Evolution of Emergent Computation SFI Technical Report 94-03-012
_[134] 웹사이트 http://www.santafe.e[...]
_[135] 문서 The Evolutionary Design of Collective Computation in Cellular Automata
_[136] 문서 Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work
_[137] 학술지 On the generation of high-quality random numbers by two-dimensional cellular automata
_[138] 문서 Cryptography with Cellular Automata
_[139] 문서 Cellular Automaton Public-Key Cryptosystem
_[140] 간행물
_[141] 간행물
_[142] 논문 "The Calculi of Emergence: Computation, Dynamics, and Induction" http://csc.ucdavis.e[...]
_[143] 논문 "Cellular Vacuum"
_[144] 논문 "The Computing Universe"
_[145] 논문 "Digital mechanics: an informational process based on reversible universal cellular automata"
_[146] 웹사이트 iLabs http://www.ilabs.it/
_[147] 서적 The Mathematics of the Models of Reference http://www.mmdr.it/d[...] College Publications
_[148] 웹사이트 Cellular Automaton http://mathworld.wol[...] 2011-03-13
_[149] 웹사이트 the Hacker Emblem page on Eric S. Raymond's site http://www.catb.org/[...]
_[150] 서적 Strange constellations: a history of Australian science fiction Greenwood Publishing Group
_[151] 서적 My mother was a computer: digital subjects and literary texts University of Chicago Press
_[152] 웹사이트 MathFiction: Bloom http://kasmana.peopl[...] 2011-03-27
_[153] 웹사이트 http://www.sfwriter.[...]
_[154] 웹사이트 http://www.dezeen.co[...]
_[155] 서적 Darwin's Dangerous Idea Penguin Books, London
_[156] 웹인용 Artificial Life Five-Creative Uses of Logic in the Invention of the Electronic Computer http://books.google.[...] MIT Press 2012-05-04
_[157] 웹인용 세포 자동차: Cellular Automata http://www.aistudy.c[...] 2012-05-04
_[158] 웹인용 초등 셀룰러 오토마타 http://pub.mearie.or[...] 2012-05-05

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com